配車計画問題
配車計画問題(Vehicle Routing Problem, VRP)参考1、2、3は、一つのデポ(拠点、倉庫)に集約された荷物を複数台のトラックを用いて配送先へ配送する際の、最適な経路を求める問題です。なにを最適の定義とするかは場合によりますが、稼働するトラックの台数やトラックの稼働時間、移動距離を最小化するのが一般的です。
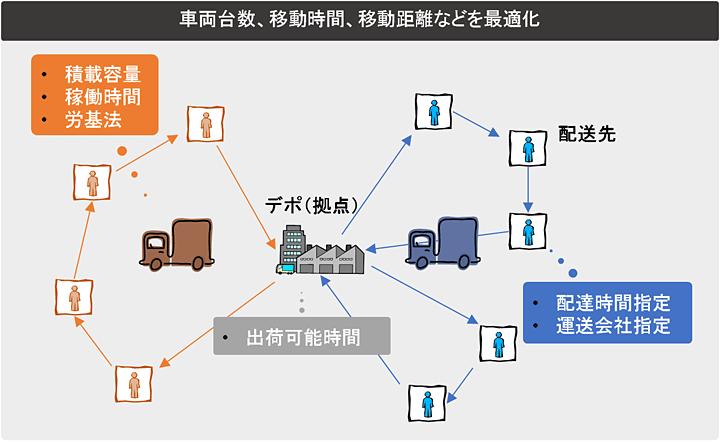
図1:配車計画問題のイメージ
トラックが一台しかない場合に移動距離を最小化するVRPは、巡回セールスマン問題(Traveling Salesman Problem, TSP)参考4、5、6と呼ばれ、デポから出発して配送先を最短距離で巡りデポへ戻る経路を求める問題です。理論的には、TSP自体が非常に難しい問題(NP困難問題)として知られていますので、それを単純なケースとして包含するVRPはさらに難しい問題となります。
VRPには付随する制約等に応じて、さまざまな拡張があります。
- デポが複数ある(Multi Depot VRP, MDVRP)
- 配送時間指定を考慮する(VRP with Time Windows, VRPTW)
- 車両の容量を考慮する(Capacitated VRP, CVRP)
こうしたさまざまな要件を考慮したVRPを総じてMulti-Attribute VRP(MAVRP)と呼びます。
なお、日本国内では労働基準法によりトラック運転手の休憩時間・労働時間などに関する規定参考7が定められているため、実用上はこれらも考慮する必要があります。また、可能な限り短時間で計算が完了することも重要です(最適化技術を実運用する際の常ですが、計算時間に対する要求はしばしば学術論文上で議論されている水準を上回るため、理論と実運用での計算時間に折り合いをつけねばなりません)。
実運用にむけては、こうした複雑な要件を考慮可能なアルゴリズムの構築が必要となります。
適応的巨大近傍探索
上述のようにMAVRPは非常に難しい問題ですので、厳密な最適化は非現実的です。そのため、なんらかの近似解法を構築するのが一般的です。ここでは、近年の研究により非常に有効であると認識されつつある、適応的巨大近傍探索(Adaptive Large Neighborhood Search, ALNS)参考8、9についてご紹介します。
ALNSはとてもシンプルなアプローチによるVRPの近似解法です。まず、適当な方法により配送計画を仮決めします。ALNSはこの配送計画に対して、配送計画の一部の除去およびその修復を繰り返すことにより配送計画の改善を続けていきます。
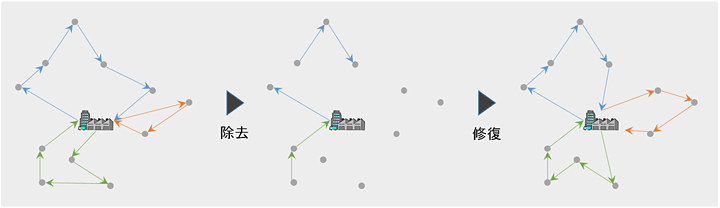
図2:ALNSの除去→修復による配送経路改善ステップ
除去の仕方は、ルートの最適性を最も阻害している配送先やルートを除去する方法や、ランダムに配送先やルートを除去する方法などさまざまな方法があります。修復の方法も同様に、除去された配送先を最もコスト(車両台数や移動距離など)を増加させないように貪欲に追加挿入していく方法などさまざまな方法があります。
ALNSには、こうしたさまざまな除去・修復方法をその都度その都度、それまでの改善履歴に応じて適応的に選択する仕組みが備わっています。
ALNSはこのようにシンプルなアプローチですが、非常に強力です。また、シンプルであるがゆえ、現実世界の多様で複雑な要件に対応することも比較的容易であるというメリットもあります。当社でもALNSをベースとした配車計画エンジンを構築し、現実的なデータに対してものの数秒〜数分のうちに良好な解(制約違反なし)を見つけ出すことに成功しています。
参考文献
- 参考1最適化メールマガジン「数理計画問題の豆知識(第18回)」(外部リンク)
- 参考2最適化メールマガジン「数理計画問題の豆知識(第8回)」(外部リンク)
- 参考3運搬経路問題(OR Wiki)(外部リンク)
- 参考4巡回セールスマン問題(NTTデータ数理システム・数理計画用語集)(外部リンク)
- 参考5驚きの数学 巡回セールスマン問題(外部リンク)
- 参考6巡回セールスマン問題への招待(外部リンク)
- 参考7トラック事業者のための労働法のポイント(PDF:92ページ, 12,203KB)(外部リンク)
- 参考8S. Kritzinger et al., "Adaptive search techniques for problems in vehicle routing, Part I: A survey", 2014(PDF:29ページ, 216KB)(外部リンク)
- 参考9D. Pisinger, S. Ropke, "Large neighborhood search", 2010




